How-to guides¶

This section contains goal-oriented guides on the features of scikit-fem.

Finding degrees-of-freedom¶

Often the goal is to constrain DOFs on a specific part of the boundary. Currently the main tool for finding DOFs is get_dofs().

>>> from skfem import MeshTri, Basis, ElementTriP2
>>> m = MeshTri().refined(2)
>>> basis = Basis(m, ElementTriP2())

(png, hires.png, pdf)

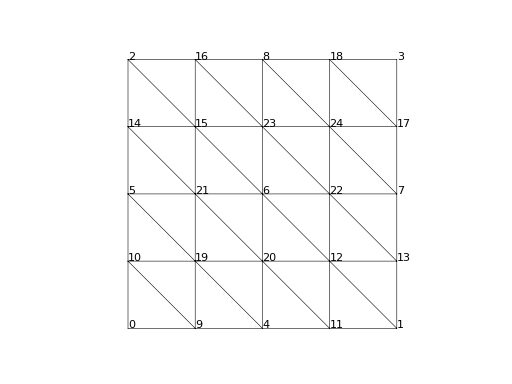
We can provide an indicator function to get_dofs() and it will find the DOFs on the matching facets:

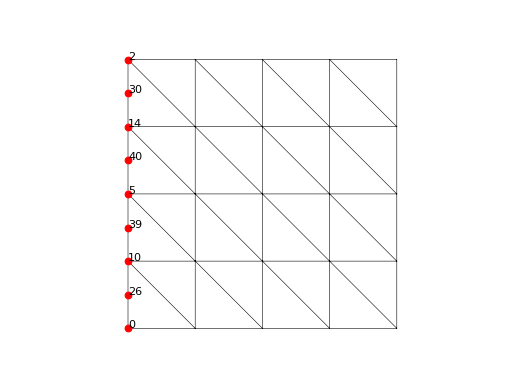
>>> dofs = basis.get_dofs(lambda x: x[0] == 0.)
>>> dofs.nodal
{'u': array([ 0,  2,  5, 10, 14])}
>>> dofs.facet
{'u': array([26, 30, 39, 40])}

This element has one DOF per node and one DOF per facet. The facets have their own numbering scheme starting from zero, however, the corresponding DOFs are offset by the total number of nodal DOFs:

>>> dofs.facet['u']
array([26, 30, 39, 40])

(png, hires.png, pdf)

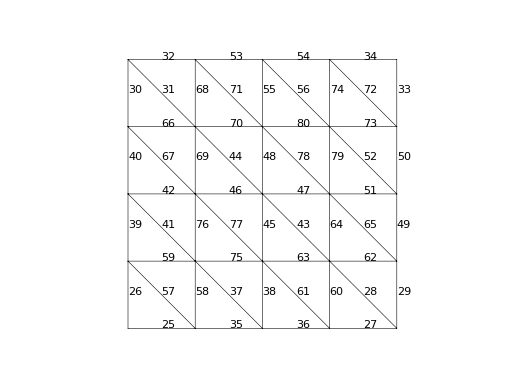
The keys in the above dictionaries indicate the type of the DOF according to the following table:

Key	Description
`u`	Point value
`u_n`	Normal derivative
`u_x`	Partial derivative w.r.t. $x$
`u_xx`	Second partial derivative w.r.t $x$
`u^n`	Normal component of a vector field (e.g., Raviart-Thomas)
`u^t`	Tangential component of a vector field (e.g., Nédélec)
`u^1`	First component of a vector field
`u^1_x`	Partial derivative of the first component w.r.t. $x$
`u^1^1`	First component of the first component in a composite field
`NA`	Description not available (e.g., hierarchical or bubble DOF’s)

An array of all DOFs with the key u can be obtained as follows:

>>> dofs.all(['u'])
array([ 0,  2,  5, 10, 14, 26, 30, 39, 40])
>>> dofs.flatten()  # all DOFs, no matter which key
array([ 0,  2,  5, 10, 14, 26, 30, 39, 40])

If a set of facets is tagged, the name of the tag can be passed to get_dofs():

>>> dofs = basis.get_dofs('left')
>>> dofs.flatten()
array([ 0,  2,  5, 10, 14, 26, 30, 39, 40])

Many DOF types have a well-defined location. These DOF locations can be found as follows:

>>> basis.doflocs[:, dofs.flatten()]
array([[0.   , 0.   , 0.   , 0.   , 0.   , 0.   , 0.   , 0.   , 0.   ],
       [0.   , 1.   , 0.5  , 0.25 , 0.75 , 0.125, 0.875, 0.375, 0.625]])

(png, hires.png, pdf)

See Indexing of the degrees-of-freedom for more details.

Performing projections¶

We can use $L^2$ projection to find discrete counterparts of functions or transform from one finite element basis to another. Suppose we have $u_0(x,y) = x^3 y^3$ defined on the boundary of the domain and want to find the corresponding discrete function which is extended by zero in the interior of the domain. You could explicitly assemble and solve the linear system corresponding to: find $\widetilde{u_0} \in V_h$ satisfying

\[\int_{\partial \Omega} \widetilde{u_0} v\,\mathrm{d}s = \int_{\partial \Omega} u_0 v\,\mathrm{d}s\quad \forall v \in V_h.\]

However, this is so common that we have a shortcut project():

>>> import numpy as np
>>> from skfem import *
>>> m = MeshQuad().refined(2)
>>> basis = FacetBasis(m, ElementQuad1())
>>> u0 = lambda x: x[0] ** 3 * x[1] ** 3
>>> u0t = basis.project(u0)
>>> np.abs(np.round(u0t, 5))
array([1.0000e-05, 8.9000e-04, 9.7054e-01, 8.9000e-04, 6.0000e-05,
       6.0000e-05, 1.0944e-01, 1.0944e-01, 0.0000e+00, 2.0000e-05,
       2.0000e-05, 2.4000e-04, 8.0200e-03, 3.9797e-01, 3.9797e-01,
       2.4000e-04, 8.0200e-03, 0.0000e+00, 0.0000e+00, 0.0000e+00,
       0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00])

(png, hires.png, pdf)

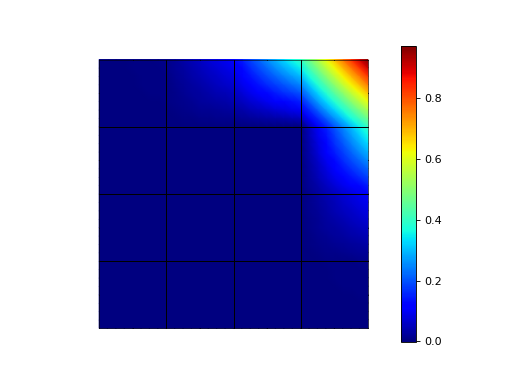
We can also project over the entire domain:

>>> basis = Basis(m, ElementQuad1())
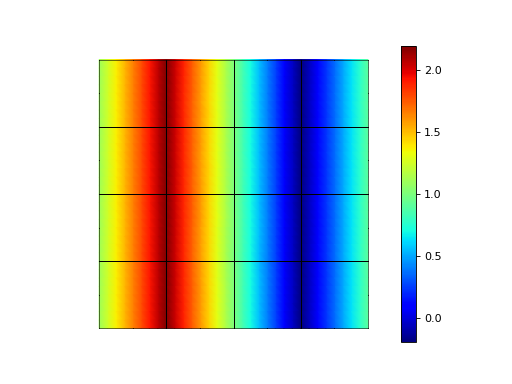
>>> f = lambda x: np.sin(2. * np.pi * x[0]) + 1.
>>> fh = basis.project(f)
>>> np.abs(np.round(fh, 5))
array([1.09848, 0.90152, 0.90152, 1.09848, 1.     , 1.09848, 0.90152,
       1.     , 1.     , 2.19118, 1.09848, 0.19118, 0.90152, 0.90152,
       0.19118, 1.09848, 2.19118, 1.     , 2.19118, 0.19118, 1.     ,
       2.19118, 0.19118, 0.19118, 2.19118])

(png, hires.png, pdf)

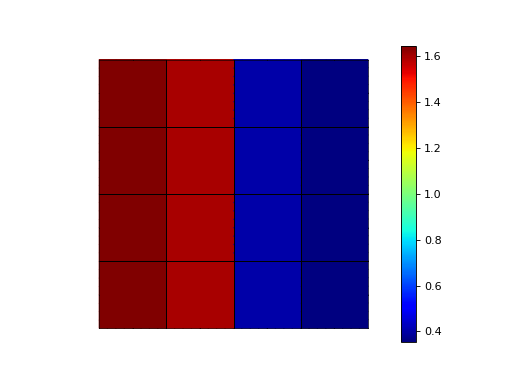
We can project from one finite element basis to another:

>>> basis0 = basis.with_element(ElementQuad0())
>>> fh = basis0.project(basis.interpolate(fh))
>>> np.abs(np.round(fh, 5))
array([1.64483, 0.40441, 0.40441, 1.64483, 1.59559, 0.35517, 0.35517,
       1.59559, 1.59559, 0.35517, 0.35517, 1.59559, 1.64483, 0.40441,
       0.40441, 1.64483])

(png, hires.png, pdf)

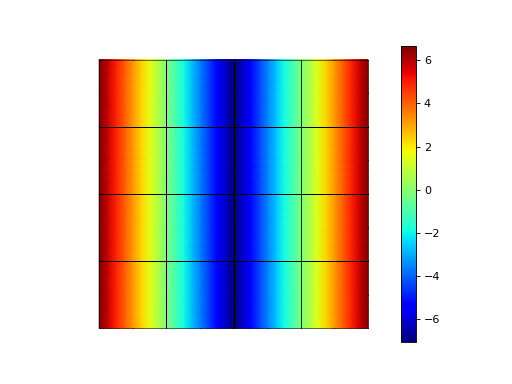
We can interpolate the gradient at quadrature points and project:

>>> f = lambda x: np.sin(2. * np.pi * x[0]) + 1.
>>> fh = basis.project(f)  # P1
>>> fh = basis.project(basis.interpolate(fh).grad[0])  # df/dx
>>> np.abs(np.round(fh, 5))
array([6.6547 , 6.6547 , 6.6547 , 6.6547 , 7.04862, 6.6547 , 6.6547 ,
       7.04862, 7.04862, 0.19696, 6.6547 , 0.19696, 6.6547 , 6.6547 ,
       0.19696, 6.6547 , 0.19696, 7.04862, 0.19696, 0.19696, 7.04862,
       0.19696, 0.19696, 0.19696, 0.19696])

(png, hires.png, pdf)

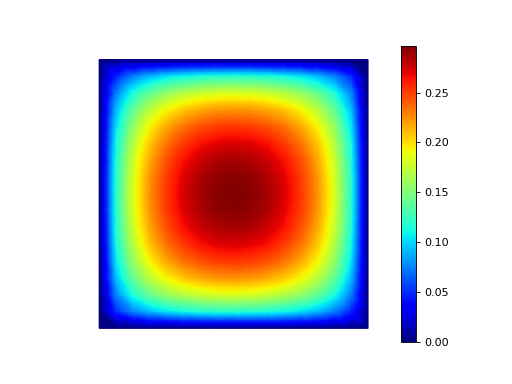
Discrete functions in forms¶

We can use finite element functions inside the form by interpolating them at quadrature points. For example, consider a fixed-point iteration for the nonlinear problem

\[\begin{split}\begin{aligned} -\nabla \cdot ((u + \tfrac{1}{10})\nabla u) &= 1 \quad \text{in $\Omega$}, \\ u &= 0 \quad \text{on $\partial \Omega$}. \end{aligned}\end{split}\]

We repeatedly find $u_{k+1} \in H^1_0(\Omega)$ which satisfies

\[\int_\Omega (u_{k} + \tfrac{1}{10}) \nabla u_{k+1} \cdot \nabla v \,\mathrm{d}x = \int_\Omega v\,\mathrm{d}x\]

for every $v \in H^1_0(\Omega)$. The bilinear form depends on the previous solution $u_k$.

>>> import skfem as fem
>>> from skfem.models.poisson import unit_load
>>> from skfem.helpers import grad, dot
>>> @fem.BilinearForm
... def bilinf(u, v, w):
...     return (w.u_k + .1) * dot(grad(u), grad(v))

The previous solution $u_k$ is interpolated at quadrature points using interpolate() and then provided to assemble() as a keyword argument:

>>> m = fem.MeshTri().refined(3)
>>> basis = fem.Basis(m, fem.ElementTriP1())
>>> b = unit_load.assemble(basis)
>>> x = 0. * b.copy()
>>> for itr in range(20):  # fixed point iteration
...     A = bilinf.assemble(basis, u_k=basis.interpolate(x))
...     x = fem.solve(*fem.condense(A, b, I=m.interior_nodes()))
...     print(round(x.max(), 10))
7278262868
1956340215
3527261363
2745541843
3065381711
2921831118
298384264
2956587119
2968478347
2963273314
2965548428
2964553357
2964988455
2964798184
2964881386
2964845003
2964860913
2964853955
2964856998
2964855667

(png, hires.png, pdf)

Note

Inside the form definition, w is a dictionary of user provided arguments and additional default keys. By default, w['x'] (accessible also as w.x) corresponds to the global coordinates and w['h'] (accessible also as w.h) corresponds to the local mesh parameter.

Assembling jump terms¶

The shorthand asm() supports special syntax for assembling the same form over lists of bases and summing the result. The form

\[b(u,v) = \sum_{E \in \mathcal{E}_h} \int_{E} [u][v]\,\mathrm{d}s\]

with jumps $[u] = u_1 - u_2$ and $[v] = v_1 - v_2$ over the interior edges can be split as

\[b(u,v) = \sum_{E \in \mathcal{E}_h} \left(\int_{E} u_1 v_1\,\mathrm{d}s - \int_{E} u_1 v_2\,\mathrm{d}s - \int_{E} u_2 v_1\,\mathrm{d}s + \int_{E} u_2 v_2\,\mathrm{d}s\right)\]

and normally we would assemble all of the four forms separately.

We can instead provide a list of bases during a call to skfem.assembly.asm():

>>> import skfem as fem
>>> m = fem.MeshTri()
>>> e = fem.ElementTriP0()
>>> bases = [fem.InteriorFacetBasis(m, e, side=k) for k in [0, 1]]
>>> jumpform = fem.BilinearForm(lambda u, v, p: (-1) ** sum(p.idx) * u * v)
>>> fem.asm(jumpform, bases, bases).toarray()
array([[ 1.41421356, -1.41421356],
       [-1.41421356,  1.41421356]])

For an example of practical usage, see Example 7: Discontinuous Galerkin method.

How-to guides¶

Finding degrees-of-freedom¶

Performing projections¶

Discrete functions in forms¶

Assembling jump terms¶

scikit-fem

Navigation

Related Topics